применения метода
В качестве примера применения предложенного метода маскировки мы выбрали небольшую программу, которая решает задачу о 8 ферзях. Текст этой программы приведён на рис. 10.

Рис. 10. Программа, решающая задачу о "8 ферзях"
Для маскировки мы выберем основную функцию queens этой программы. Граф потока управления функции queens приведён на рис. 11.
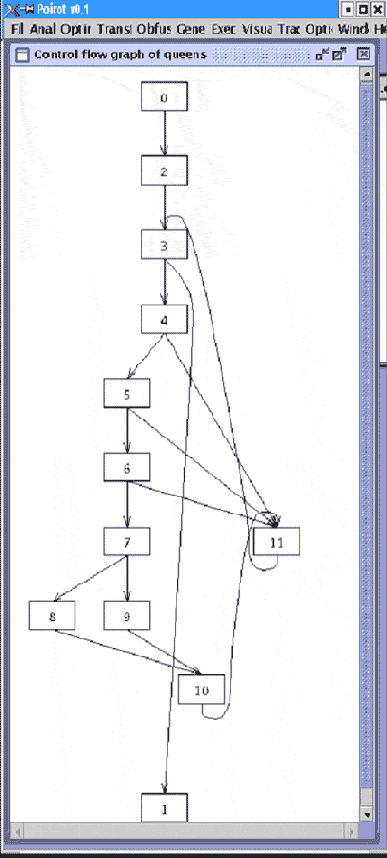
Рис. 11. Граф потока управления функции queens
Результат маскировки функции queens приведён ниже.
static void queens(int c) { int q[13u]; q[10] = 0; q[8] = 0; q[1] = (c + 7); q[4] = 0; q[7] = 0; q[2] = -1; q[11] = 0; L127: if (!q[2]) goto L128; q[11]++; q[2] = (unsigned) q[2] >> 1; goto L127; L128: q[12] = q[11]+q[2]-19; q[11] = q[11] % q[12]; L111: if (q[q[11]+4] >= 8) goto L45; q[3] = q[10]; q[q[11]+2] = ((q[8] + q[7]) + 1); q[9] = (q[10] + 1); q[1] = ((q[1] + c) + 2); q[q[11]+4] = (q[10] + 2); q[7] = ((7 + q[q[11]+2]) - q[1]); if ((v3)[q[3]] == 0) goto L94; q[4] = ((v8)[q[3]] + (v2)[((q[3] - c) + 7)]); if ((v7)[((q[3] - c) + 7)] == 0) goto L94; if (q[7] < 0) goto L96; if (q[7] 5); if ((v3)[q[9]] == 0) goto L111; if ((v7)[((q[9] - c) + 7)] != 0) goto L112; if (q[1] != 0) goto L111; if (q[4] (v6)[(q[2] + 1)]) goto L122; (v2)[(q[9] + c)] = ((v6)[q[2]] + c); q[8] = (((q[1] + q[4]) + q[9]) - 7); (v4)[(q[9] + c)] = 1; q[4] = (v8)[q[9]]; (v8)[q[9]] = 1; (v7)[((q[9] - c) + 7)] = 1; q[7] = (q[7] - 1); (v3)[q[9]] = 1; q[q[11]+5] = (q[11] + q[12]) % 13; goto L111; L45: ; }
Граф потока управления замаскированной функции приведён на рис. 12. На рисунке графа дуги, получившиеся при выполнении преобразования зацепления дуг, имеют большую толщину, а соответствующие базовые блоки выделены серым цветом.
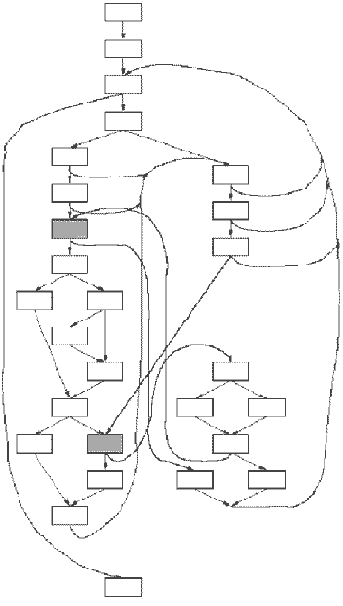
Рис. 12. Граф потока управления замаскированной функции queens
В таблице 1 приведены метрики сложности кода для исходной функции queens и для её замаскированного варианта. У замаскированной функции значения всех метрик, кроме метрики сложности графа вызовов выше, чем у исходной функции. Принципы предлагаемого метода маскировки нашли отражение в примере следующим образом:
| Таблица 1. Изменение метрик сложности для замаскированной функции queens | ||
| метрика | исходная функция | после преобразования |
| CC (Цикломатическая сложность) [14] | 6 | 21 |
| FC (Сложность по связям) [13] | 9 | 27 |
| GC (Сложность графа вызовов) | 2 | 2 |
| SC (Структурная сложность) [13] | 3 | 24 |
| YC (Зацикленность) | 0.595 | 0.8119 |
| DC (Сложность потока данных) | 82 | 8964 |
